Le problème : comment transmettre directement le mouvement du moteur sur une roue sans utiliser d'engrenages ? Quelle puissance pour le moteur ? Quelle force ?
 Il faut bien dire que Le ROQUET m'a posé quelques problèmes et que ce n'est qu'au 4ème moteur que la petite loco a bien voulu se mouvoir correctement.
Il était donc nécessaire d'effectuer une petite recherche pour voir, si dans ce cas de transmission du mouvement directement à la roue ,il était possible de prévoir le moteur adéquat ... et d'éviter les errements connus dans cet
 |
|
quelques exemples de transmission directe
transmission appliquée aux roues motrices d'une locomotive par un moteur oscillant.
Photos issues d'une banque de photos de Google. |
|
|
|
|
 |
problème de Forces | les forces opposées en présence
|
|
- la balançoire dans une position d'équilibre :
A - F1 x r1 = F2 x r2
B - F1 x r1 = F2 x r2
Si on modifie r1 et r2, on modifie F1 et F2. |
|
C . pour obtenir le mouvement souhaité, il va falloir vaincre le couple Fr x rr avec un couple Fm x rm plus important.
Fm = Force moteur Rm = rayon moteur Fr = Force résistante Rr = rayon résistant |
|
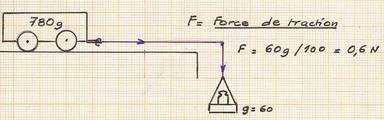 la force de traction
C'est un couple facile à mesurer expérimentalement.
Dans le cas du Roquet, à 60 grammes placés dans le plateau, la loco se met à avancer, on vient de rompre le point d'équilibre des forces..
60 g équivalent à 0.6 Newton (1 kg-force = 9.91 Newton et 100 g = 1 newton -arrondi).
Le couple à la roue est alors :
F (N) x r (rayon de la roue en mètres) = 0.6 x 0.025 = 0.015 N |
|
- de la force de traction à la force de résistance
La valeur obtenue est celle d'un couple minimum et, pour mes calculs qui ne sont qu'indicatifs, on peut imaginer qu'il représente le couple résistant
Il restera donc à calculer le couple moteur pouvant le vaincre et, évidemment supérieur. |
|
Il n'est pas toujours évident d'évaluer précisément la force de traction au début d'une construction et pourtant c'est elle qui va déterminer en grande partie les caractéristiques du moteur et la puissance que l'on pourra en obtenir.
On peut avoir une idée de la masse de l'engin en construisant le châssis, en installant les roues, la chaudière et ses accessoires ainsi que des bouts de métaux à usiner représentant ... tout le reste, d'une manière peu précise. |
|
Pour un autre projet , celui de la Belle Taravana, j'ai envie d'essayer ce truc :
La force de résistante est F = k x P
. F en Newton
. k = le coefficient de frottement et pour des roues d'acier sur des rails la valeur varie entre 0.5 et 1 (on prendra 0.75)
. P = m.g : masse en kg (0.8 pour le Roquet) x g (pesanteur)
|
|
Là je me permets encore une supposition en disant que, lorsque ma loco ne bouge pas, la force de résistance équivaut à une force d'inertie.
En fait on a bien des difficultés à s'y retrouver. Voici ce que je lis :
"En mécanique newtonienne, il existe deux types de masse, la masse pesante (m.p) et la masse inerte (m.i).
. la masse pesante : dans un champ de gravitation g, le poids d'un objet est P = m(p) x g
. la masse inerte est la mesure de l'inertie d'un objet c'est à dire de la difficulté à lui communiquer une accélération 'a = f / m(i) et F = m(i) x a
. Newton a constaté que ces deux masses étaient égales, sans conclusion physique
Dans les deux cas, a = g." |
|
Et si, dans le cas présent, on considérait qu'on se trouve à un moment où il n'y a aucune accélération (ce qui est d'ailleurs exact !) ?
Alors on se trouverait devant :
F = k x masse = 0,75 x 0.8 = 0.6
Coup de chance probablement que ce résultat identique !
|
|
le moment d'une force
Il dépend de l'axe de rotation : c'est le produit de l'intensité de la force (que l'on peut calculer) et la distance entre l'axe et le point d'application de la force (que l'on peut déterminer).
- intensité de la force crée par le moteur : P (watts) = F (N) x Vitesse en m/s et F = P x V
- incidence du levier si F = 1,5 N
. en A, F x 0 = 0 : F s'applique à un point immobile m^me en rotation et ne peut pas s(exprimer
. en B , F x 0.004 = 0.006 N
. en C , F x 0.002 = 0.03
"Le levier amplifie ou réduit l'effort proportionnellement au rapport du bras de levier c'est à dire la distance de l'axe au point d'application de la force(longueur du levier)." |
|
|
|
|
|
application à un véhicule | le moteur et les forces en présence sur Le ROQUET |  |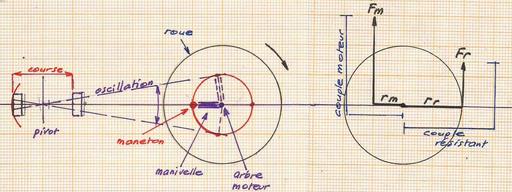
|
le moteur
On pourra en faire varier la puissance en modifiant sa cylindrée et sa course.
Il faut aussi se fixer une pression d'utilisation et une vitesse de fonctionnement.
Pour le Roquet, la pression choisie est de 2 bars, la vitesse est de 1.5 km/h et, avec des roues de 5 cm de diamètre on aura une vitesse de 159 tr/mn et de 2.65 tr/s
Vitesse sur le circuit : 150 tr/mn donc 2.5 tr/s qui seront pris en considération.
Une fois le moteur construit, on se retrouve avec deux modifications envisageables : la pression et la vitesse. Autant ne pas trop se tromper si on ne veut pas en construire un autre ... |
|
Le ROQUET - moteur version 4
. roue de 5 cm de diamètre, 0,157 m de circonférence
. 150 tr/mn ; Vitesse en m/s = 0.3945
. moteur de 4.8 cm3 : alésage 0.8 cm, course de 2.4 cm
. puissance réelle de 0.48 watts
. couple de résistance (traction) de 0.6 N
. couple moteur de 0.03 N supérieur au couple à la roue
. couple à la roue de 0.015 N
- comparaison des forces en présences :
. calcul de Fm (force motrice) pour être à une position d'équilibre :
Fm x Rm = Fr x Rr
Fm x 0.012 = 0.6 x 0.025 = 0.15 N et
Fm = 0.015 / 0.012 = 1.25 N
- or P = Fm x V ms et F = P / Vms et Fm = 0.48 / 0.3945
Fm = 1.223 N qui est inférieure à la force nécessaire pour vaincre l'équilibre , force de 1.25 N
On en est très proche mais ce n'est pas suffisant et explique probablement pourquoi Le Roquet avait des difficultés à absorber les inégalités du circuit.
|
|
Le ROQUET - moteur version 5
. roue de 5 cm de diamètre, 0,157 m de circonférence
. 150 tr/mn ; Vitesse en m/s = 0.3945
. moteur de 4.2 cm3 : alésage 0.8 cm, course de 2.6 cm
. puissance réelle de 0.52 watts
. couple de résistance (traction) de 0.6 N
. couple moteur de 0.033 N supérieur au couple à la roue
. couple à la roue de 0.015 N
- comparaison des forces en présences :
. calcul de Fm (force motrice) pour être à une position d'équilibre :
Fm x Rm = Fr x Rr
Fm x 0.013 = 0.6 x 0.025 = 0.15 N et
Fm = 0.015 / 0.013 = 1.154 N
- or P = Fm x V ms et F = P / Vms et Fm = 0.52 / 0.3945 et
Fm = 1.318 N qui est supérieure à la force nécessaire pour vaincre l'équilibre , force de 1.154 N
Le levier a été allongé, la course s'en est trouvée modifiée et cette fois Le Roquet devrait s'exprimer sans ses soucier des inégalités du circuit.
En fait il me semble que la longueur du levier doit être égale au rayon de la roue, voire légèrement supérieure. Ce qui a une incidence sur la course du piston. |
|
application à une embarcation | La résistance à l'avancement d'un bateau dépend d'un certain nombre de facteurs.
Cette étude a déjà été menée et s'est trouvée facilitée grâce aux feuilles de calculs de Jean-Marie TRIVIDIC que l'on trouvera à la fin de cet
| | album |
|
Comme dans le cas précédent, il doit donc être possible de concevoir le meilleur moteur possible pour obtenir la force capable de vaincre le couple de résistance et faire avancer le steamer ... |
|
A suivre un jour : celui où je me lancerai dans cette construction ... |
|
|
 album en construction...Des erreurs ? Des commentaires ? Des questions ? ... écrivez-moi |
| | | | |
|
