Généralement, quand on se met à construire, on commence par un moteur ou une coque ... on installe une hélice, une chaudière et ... ça fonctionne plus ou moins bien !
|
C'est ce que j'ai fait comme beaucoup.
D'autres démarches, moins improvisées peuvent être envisagées. Une invitation à vous faire profiter de mes lectures.
... en partant d'un coque, quelques points sur lesquels se pencher
. le choix se portera sur un modèle assez rapide comme une chaloupe ou encore sur un modèle au déplacement majestueux et beaucoup plus lent comme un remorqueur
. le poids sera fonction de la taille du modèle
. la vitesse, à l'échelle, devra être réaliste
. l'hélice sera choisie en fonction de la vitesse à obtenir et il faudra en connaître le pas
. le nombre de tours à obtenir de notre moteur et donc sa cylindrée, sa puissance et la pression à fournir
. la chaudière pour maintenir la pression
...en partant d'un moteur
la démarche sera à l'inverse mais les mêmes points seront à examiner |
|
 l'hélice | parce qu'il faut bien commencer par quelque chose !
trouver le PAS de l'hélice
La méthode assez simple décrite est inspirée par un article de Micéa POPESCU paru dans le MRB n° 217 de janvier 1981.
On imagine que le commerçant n'en donnait pas le pas. C'est ce qui m'est arrivé ... ou alors j'ai oublié ! |
|
 Tracer un cercle égal au diamètre (D) de l'hélice - cercle joignant le sommet des pales :
ici, D = 74 mm
Tracer un autre cercle dayant un diamètre de 0.7 D:
ici, d = 52 mm |
|  Découper 2 petites équerres en carton et les placer de part et d'autre d'une pale, à la verticale de d :
|
|
|
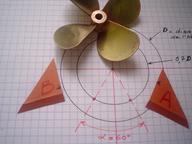 . noter le point bas de B et celui de A projeté sur d
. cocher sur B et A le point de rencontre avec la pale
. enlever l'hélice puis unir les points tracés à partir du centre et mesurer l'angle formé :
ici, α = 60° |
|  . mesurer la distance entre les points portés sur B et A :
ici, on trouve 10 mm |
|
|
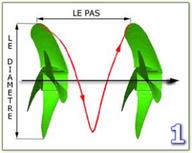
calcul du PAS géométrique H
H : H = (A - B) . 360 / α
ici, H = 10. 360 / 60 = 60
"L'angle réel du PAS n'est pas le même tout au long de la pale, on apprécie sa valeur par le rapport du pas avec le diamètre de l'hélice : H/D " :
et ici on obtient PAS = H : D = 60 / 74 = 0.81
Sachant que le meilleur rapport pour une hélice se trouve situé entre Pas = 0.8 ... 1.5, c'est tout bon !
|
|
| Un tableau dressé par le même auteur et que l'on trouvera dans le même numéro : des renseignements sur l'hélice mais d'autres comme la vitesse en noeuds, le nombre de tours-minute et le nombre de pales : |  |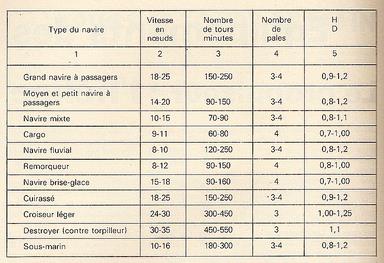
|  | Si je possédais cet appareil à mesurer le pas des hélices de diamètre 20 à 120, construit par Jean-Pierre PHILIPPE, après utilisation et relevés, j'appliquerais sa formule et obtiendrait :
L = H1 (A) - H2 (B) = 10
et pour obtenir le pas P avec un angle de palpage de 60° , P = L x 6 = 60
soit le même résultat .
La description de ce magnifique outil se trouve dans le MRB n° 302 de novembre 1988 !
|
|
|
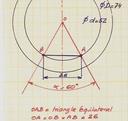
Il est aussi possible d'appliquer une autre formule trouvée chez Léonard SUYKENS.
On ajoute la mesure au réglet ou par le "calcul" de la corde formée par l'angle α : ici 26 mm
et on applique cette formule : P = 2,2 . D . (A - B) / 26 ce qui donne : P = 2.2 . 74 . 10 / 26 = 60 ... et c'est encore la même chose !
|
|
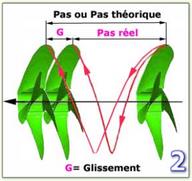 le glissement
Connaissant le pas de l'hélice, on pense pouvoir calculer la vitesse de notre bateau ... Mais, cette vitesse est moindre : l'hélice n'avance pas par tour de la distance indiquée par le pas théorique obtenu.
Il faut introduire la notion de glissement qui dépend de la forme de la coque .
Le pas est la distance théorique qu'une hélice devrait parcourir pendant 1tour si elle tournait dans un solide : mais l'eau n'est pas un solide, il se produit des pertes.
Là est la différence entre le pas théorique et la distance réellement parcourue : cette différence est le glissement ou le recul."( Mar LAMOUR dans MRB 318.
Coefficients trouvés :
. coque à déplacement : remorqueur, chalutier > 35 à 50 %
. bateau rapide > 25 %
|
|
nombre de pales d'une hélice | 
Ici intervient la notion du masquage où l'hélice ne reçoit pas de façon égale sur ses pales l'écoulement de l'eau, une ou des pales se trouvant masquées par la quille ce qui va provoquer un déséquilibre.
La mailleure solution en modélisme semble d'adopter une hélice à 4 pales, les "turbulences de l'eau n'agissant que sur 2 pales à la fois. |
|
|
| pas à gauche et pas à droite d'une hélice | Si on en monte une seule, elle peut être "à droite" : elle tourne dans le sens horaire en marche avant ; ou "à gauche" qui tournera dans le sens inverse.
Par contre, si on en installe deux, elles doivent être de pas contraire pour contrer l'effet de couple.
Comment les différencier ?
Regarder l'hélice par le dessus : si les pales montent vers la gauche elle est de pas à gauche (photo de gauche) ; si elles montent vers la droite, elle est de pas à droite (photo de droite).
Les photos sont extraites de cette page ::
http://www.sisl.ch/_popup/helice1.htm
|
| |
|
Pas évident comme me le fait remarquer Laurent.
Voici 2 hélices que l'on trouve chez un détaillant : l'une est dite à gauche et l'autre à droite !
C'est noté, heureusement, car la photo n'append rien. |
| | |
Alors peut-être que ces documents trouvés sur le Web seront utiles.
Mais, finalement, ce que je préfère, c'est le truc du tire-bouchon ! |
|
|
 | | pas à gauche : la spire part du bas et monte à gauche |
|  | | hélice pas à gauche (senestre) |
|  | | pas à droite: la spire part du bas et monte à droite |
|  | | hélice pas à droite (dextre) |
|  | | mon hélice monte à droite ... |
|  | | ... tout comme le tire-bouchon ! |
|
|
| | Et si nos pales ne suivent pas la direction de l'hélice du tire-bouchon qui lui est à droite, notre hélice sea réputée à gauche ! |
|
|
diamètre de l'hélice
"Une grande hélice tournant lentement est plus efficace qu'une petite hélice tournant à haute vitesse : la raison d'être d'une hélice est de donner une accélération à l'eau qui y pénètre; il est possible d'accélérer un petit volume d'eau à grande vitesse ou un grand volume d'eau à petite vitesse et d'avoir la même poussée.
Cependant, le 2ème système est le meilleur."" ( Simon HIGGINS dans MRB 324)
Quand on possède un plan, aucun problème car on se réfère au diamètre donné ...
|
|
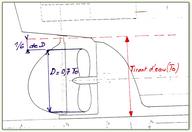
... mais si on dessine ses plans, voici les proportions trouvées qui peuvent guider dans l'installation de l'étambot et le calcul du diamètre de l'hélice en partant du To.= tirant d'eau qui est la distance en mètres entre la surface et le point le plus bas du navire et, pour nous, des cm ou mm.
Voir également :
http://fr.wikipedia.org/wiki/Tirant_d'eau |
|
Sur ce croquis qui représente l'arrière de la chaloupe de Bernard Rétif, To = 66 mm
et le diamètre de l"hélice devrait être de To . 0.7 = 66 . 0.7 = 46
Le choix de BR se porte sur une hélice de 40 à 50 !
|
|
|
|
|
Petites observations :
. ma chaloupe présente une légère vague d'étrave et se déplace de façon réaliste alors que je marche à vitesse normale sur la berge, donc elle doit avancer à la vitesse de 3 ou 4 km/h
. mon cargo avance à la même vitesse, présente la même vague, mais son allure n'est pas réaliste (il faut dire qu'il n'est pas dans ses lignes d'eau !)
|
| |
|
Quand on connaît la vitesse réelle de la maquette, on peut calculer la vitesse à l'échelle en appliquant cette formule qui, à mon avis, a des limites :
vitesse à l'échelle = vitesse réelle / racine de l'échelle
Exemple: un remorqueur est affiché pour une vitesse de 10 noeuds et il est construit à l'échelle du 1/24èm, quelle doit être sa vitesse à l'échelle ?
. 1noeud = 1852 m en 1 heure
. vitesse du modèle = 10 . 1852 / racine de 24 = 3780 m/h ou 3.8 km/h ce qui ne me semble déjà pas très réaliste !
et si mon modèle est au 1/8ème , je dépasse les 6 km/h !!!
Là encore, il vaut mieux se baser sur l'expérience. |
|
Pour un remorqueur qui utiliserait l'hélice qui a servi pour cette recherche, on pourrait facilement imaginer, une vitesse réaliste minimum de2 km/heure ...
Il faudra qu'il puisse parcourir au minimum 2000m en 1 heure ou encore 0.555 m/seconde et encore 555 mm/seconde.
Théoriquement, notre hélice devra faire : 555 / 60 (pas théorique de l'hélice) = 9.25 tours par seconde ou 925 . 60 = 555 tours par minute .
Mais, freinée, pour parcourir la même distance, il faudra : 555 tours + glissement (50 % retenues) = 555 + (555 . 0.5) = 832.5 tours à la minute
Pour calculer la vitesse théorique, on peut aussi appliquer cette formule :
Vitesse = R . P . 60 / 2 200 000
où V est en km / h ; R le régime maximum en tr / mn et P est le pas théorique de l'hélice en mm
Pour obtenir la vitesse réelle, il faudra appliquer le coefficient de glissement ou de recul ou de perte ... (Bernard GILLIER dans MRB 388)
|
|
Je viens de recevoir une aimable contribution de V.DahliaBleue qui m'écrit :
"Ce n'est pas à proprement parler une erreur, mais plutôt une incertitude.
Dans le paragraphe "la vitesse à l'échelle", après avoir calculé avec pertinence la vitesse théorique de la maquette du remorqueur (de dix nœuds réels) vous doutez de l'aspect réaliste du résultat.
Que ce soit à l'échelle du 1/24èm(3,8 km/h) ou au 1/8ème (6 km/h), ces vitesses maquette vous paraissent excessives. Elles sont pourtant conformes à la fameuse similitude de Froude, qui est donnée par la formule que vous avez appliquée.
Vous auriez sans doute préféré appliquer l'échelle directe, c'est-à-dire V maquette = V réel divisée par échelle. Ça aurait eu pour effet de faire avancer la maquette plus lentement.
Si le vrai navire parcourt sa longueur en dix secondes, par exemple, on s'attend en effet à ce que la maquette en fasse autant. Mais c'est alors extrêmement lent (dans les cas cités, au 1/24èmce sera 0,42 nœuds (0,77 km/h) ou au 1/8ème , 1,25 nœuds (2,32 km/h).
La similitude de Froude prend en compte des éléments qui ne sont pas réductibles à l'échelle : densité du milieu aquatique, sa viscosité… ce qui finalement rend assez réaliste la navigation du modèle."
Un grand remerciement pour cette précision qui me permet d'ajouter un lien que je tenais en réserve ...
http://francois.lonchamp.free.fr/Froude/Nombre%2520de%2520Froude.html
|
|
le poids du bateau, son déplacement | Dans la notice concernant le navire réel, on peut parfois trouver ce genre d'inforamtion : déplacement = 100 T, que l'on peut traduire par 100 000 kg et, pour calculer le poids de notre modèle, on appliquera la formule :
Poids du modèle = Poids réel / échelle 3
Et si notre modèle est au 1/20ème , on aura un poids de 100 000 / 203 = 12.5 kg
|
|
 Quand on ne possède pas ce renseignement, on peut procéder ainsi :
Imaginer la coque sur le plan d'eau -lesté pour atteindre la ligne de flottaison- et relever ses dimensions : Longueur immergée, largeur au maître bau immergée et hauteur de la quille à la ligne de flottaison.
Le volume obtenu : L . l . h sera à multiplier par un coefficient appelé coefficient de finesse ou prismatique.
Si nous obtenons 15 dm3ou encore 15 kg d'eau, c'est le poids du modèle qui est parfaitement égal à la poussée d'Archimède et on obtient le "déplacement" : en fait le déplacement, c'est le poids.
Coefficients de déplacement trouvés :
. coque élancée = 0.38 à 0.40
. type remorqueur = 0.45 à 0.50
. type pétrolier = 0.70 à 0.74
Et pour cet exemple, le poids ou déplacement du modèle, s'il s'agit d'un remorqueur, sera de : 15 . 0.50 = 7.5 kg
Un lien vers le site de mon ami Eric GAUTHIER qui a déjà traité de ce problème à propos du lestage d'un bateau et qui explique parfaitement ce qu'est la poussée d'Archimède :
http://maquettes.ge.pagesperso-orange.fr/article/pages/page8n12.htm |
|
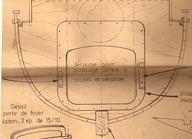
Pour cette chaloupe, on peut appliquer un coefficient de finesse de 0.40 car elle fait plus de 1 m de longueur pour 14.5 cm seulement au maître bau. |
| 
Par contre, pour cette pinasse, genre de petit remorqueur ou bateau de service à Hambourg, la longueur est de 1.2 m pour 34,.5 cm au maître bau, et pour le coefficient de finesse, on choisira 0.5.. |
|
|
le gouvernail | En partant d'un plan, on suit le dessin donné, et sans plan ...
on augmente la surface du gouvernail du bateau réel de 10 à 15% pour pouvoir manoeuvrer correctement.
(souvenir ancien mais impossible de retrouver les références !) |
|
la recherche de l'allure idéale | | Pour bien faire, on devrait avoir sur l'eau une embarcation qui ... |
|
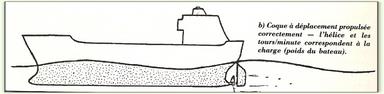 | | ... ressemblerait à ceci ... |
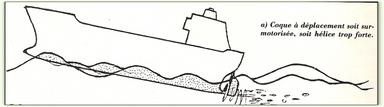|  | | ... et non à cela ...! |
|
|
| (2 dessins de Simon HIGGINS dans MRB n° 324) |
|
la cylindrée du moteur |  Beaucoup de lectures plus ou moins ardue pour finalement tomber sur celle-ci a le mérite de la simplicité.
Elle est extraite d'un cahier de Léonard SUYKENS :
Cylindrée en cm3 = L . B . P / α
ou L = la longueur à la flottaison, B = la largeur au maître bau, P = la profondeur à partir de la flottaison, le tout en cm.
α est un coefficient dépendant d la longueur du bateau.
Pour α Léonard Suskens prend en compte les valeurs hollandaises qu'il majore de 20% :
. 4350 pour 75 cm
. 4000 pour 90 cm
. 3900 pour 100 cm
. 3600 pour 120 cm
. 3300 pour 140 cm
. 3000 pour 150 cm
Et il calcule ainsi pour un bateau de L = 100 cm, B = 26 cm, P = 9 cm, α = 3900
> cylindrée en cm3 = 100 . 26 . 9 / 3900 = 6 cm3 et 6 cm3 . 1.2 (majoration de 20%) = 7.2 cm3
J'ai fait quelques calculs et mon moteur devrait tenir la route pour emmener la pinasse de Hambourg ...
|
|
la chaudière | Quand on a collationné tous les résultats possibles, il devient facile de calculer la surface de chauffe nécessaire à notre chaudière ... et donc sa taille pour alimenter correctement notre bateau.
Petit problème déjà étudié dans cet album :
| | généralités sur les chaudières |
|
fabriquer son hélice | Je n'ai pas l'ambition, pour l'instant ,de me lancer dans cette aventure.
Voici cependant 2 pistes :
|
|
. Le meilleur document trouvé pour la construction d'une hélice : un pas à pas (et pale à pale) de Jean-Pierre PHILIPPE paru dans le numéro 301 d'octobre 1988 de MRB.
Une méthodologie, un outillage spécifique et des instruments de mesure dont celui déjà montré précédemment. |
|
. une construction dans la masse de Marcel LAVIEqui me fait le plaisir de m'envoyer l'article qui présentait sa méthode et que l'on peut télécharger dans la page des téléchargements sous le titre : fabrication des hélices dans la masse.
C'est aussi l'occasion de visiter la galerie de Marcel, un modéliste hors du commun :
http://www.modelismeenpolynesie.com/anne/index.html
|
|
. une autre construction super détaillée sur cette page :
http://bateaux.trucs.free.fr/ageneral.html
Alain venant de changer de fournisseur d'accès, la page s'ouvre sur le sommaire général : descendre en bas de la page, voir les "réalisations de Guy" et cliquer sur l'image de l'hélice ... |
|
 pour en savoir davantageUn album est lancé et des informations complémentaires arrivent.
En voici une très technique mais abordable où on en apprendra encore bien plus sur la propulsion des bateaux : un cours sur la propulsion par hélice de Stéphane CORDIER.
J'aimerais entrer en contact avec Monsieur Cordier. Si vous le connaissez ...
Un autre document à télécharger dans la page des téléchargements. |
|
quelques croquis supplémentaires | | Le sujet passionne et de nouveaux documents arrivent comme ceux-ci dont on peut tirer profit. |
|
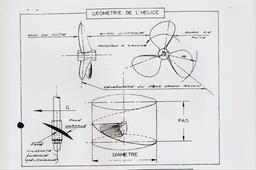 | | l'hélice, un vocabulaire qui lui est propre |
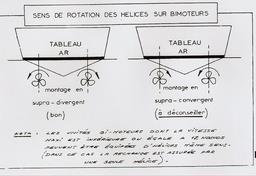|  | | rotation avec deux hélices |
|  | | un peu différent de ce que j'avais noté ... |
|
|
 différents types d'hélices du commerce
Découvert dans le dernier catalogue de MULTIREX (matières premières) les hélices de la marque Raboesch : toute une gamme permettant d'équiper n'importe quel type d'embarcation ...
Multirex - BP 65217 - 44352 Guérande Cedex
www.multimatieres.fr |
|
|
|
une suite à venir ... | ... mais cela attendra un peu avec tous ces chantiers en cours !
Quand j'ai procédé à l'agrandissement de l'atelier, malgré l'espace nouveau, j'ai eu bien du mal à caser cette coque de pinasse de Hambourg de 1,2 m de longueur commencée il y a quelques années et abandonnée pour faire autre chose que des bateaux ... Elle attendait sagement sur une étagère.
Ce sera l'occasion de mettre en pratique tout ce qui est écrit ci-dessus et ensuite de calculer :
. son poids
. la vitesse à obtenir à l'échelle
. le moteur nécessaire (mais j'ai déjà mon idée)
. la surface de chauffe et la chaudière
|
|
|
la suite
avec la construction de la machinerie complète, une machinerie qui fonctionne parfaitement.
Cependant l'ensemble est devenu trop pesant pour moi et cette embarcation ne rejoindra pas le lagon, dommage de voir cette coque et sa machinerie rester sur une étagère. Mais je me suis fait bien plaisir.
La construction de la machinerie avec tous les plans est disponible dans cet |  |
|
|
|
 album terminé ... pour l'instant !Des erreurs ? Des commentaires ? Des questions ? ... écrivez-moi |
| | | | |
|
